摘要:本文介绍了一种优化193 nm抗反射(AR)涂层在强曲率球面基底上宽入射角(AOI)范围光谱性能的方法。该方法通过测量测试板上涂层厚度与石英晶体微天平上的涂层厚度之间的关系,修正了单层LaF3和MgF2薄膜在测试板上的实际厚度。在多层AR涂层中,接口粗糙度通过原子力显微镜(AFM)测量获得,并通过模拟作为均匀子层,考虑其对多层光谱的影响。AR涂层中子层的孔隙率通过逆向工程涂层/基底/涂层堆叠的剩余反射率获得。然后,将获得的折射率和厚度用于分析和优化193 nm AR涂层的光谱性能。对于强曲率球面表面,通过同时考虑球面基底不同位置的性能函数,优化了AR涂层的光谱均匀性。该工作为193 nm AR涂层在宽入射角范围和强曲率球面基底上的性能优化提供了一个通用的解决方案。
我们提供定制全国产镀膜服务(紫外(库存--13.5nmMo/Si平面反射镜(反射率63%)193nm 45度入射97.5%反射率 266nm 355nm 405nm平面反射镜和增透膜),大尺寸 600mm高功率激光反射镜可见光(二,三,四通道滤光片,半高1nm滤光片),近红外,金属反射膜(金银铜铝),窄带(近红外带宽0.3nm,可见光带宽1-2nm)),中远红外(增透膜,滤光片),也拥有大量的滤光片标品库存,请联系我的微信获取库存列表。

1. 引言
集成电路中高晶体管密度的进展要求光刻系统具有短工作波长和高数值孔径(NA)[1]。为了实现高NA,投影镜头的某些光学元件被设计为具有强曲率的凹面或凸面形状。较大的陡度导致入射角(AOI)范围宽广,能够从近轴光线的0°到偏轴光线的60°以上[2]。在这些强曲率光学元件上设计和制造高性能的抗反射(AR)涂层,要求涂层具有宽广的AOI范围,这一过程是成功制造高NA光刻系统的关键步骤,因为在这些高NA系统中,既需要高的照明均匀性,又需要低的波前误差。因此,沉积在强曲率基底上的AR涂层必须在光学性能上均匀,而这一点可以通过修正涂层厚度的均匀性来控制[3-7],同时还需设计具有宽AOI范围和广泛工作波段的AR涂层[2,3]。
目前,193 nm准分子激光仍然是光刻系统中最广泛使用的光源之一。金属氟化物[8-11],如氟化铈(LaF3)[12-15]和氟化镁(MgF2)[16,17],通常通过热蒸发法制备,分别作为193 nm光刻系统中投影镜头的高折射率和低折射率子层。在以往的研究中发现,热蒸发制备的LaF3和MgF2薄膜呈柱状微结构,表面粗糙,这通常导致单层薄膜的孔隙度随厚度增加而增加[18,19]。这种与厚度相关的薄膜孔隙度使得使用均匀的多层模型描述氟化物AR涂层的性能变得困难,并且使得使用商业软件准确设计涂层变得更加复杂[20]。此外,由于具有广泛AOI范围的193 nm AR涂层通常由多达7个子层组成,因此厚度依赖的折射率不均匀性对其光学性能的影响会被放大。
此外,氟化物薄膜的微结构和相关的光学特性与它们在强曲率球面基底上的径向位置密切相关[11]。我们此前报告过,LaF3和MgF2薄膜的柱状倾斜角从强曲率球面基底的中心到边缘逐渐增大,导致折射率不均匀性增加约一个数量级[21],这导致了AR涂层在强曲率球面基底上的光谱不均匀性。例如,193 nm处的AR涂层残余反射率在中心区域仅为0.2%,但在基底的边缘区域可高达1%[21]。尽管可以通过反复试验来优化氟化物涂层的性能,但能够直接理论设计出具有所需光谱均匀性的AR涂层的方法,对于高NA光刻系统的整体性能优化具有重要的技术意义。
本文考虑了多种因素,旨在优化193 nm AR涂层的光谱性能,这些涂层具有广泛的AOI范围并且适用于强曲率球面基底。通过实验建立涂层厚度与石英晶体微天平和行星旋转基底上薄膜厚度之间的关系,精确控制薄膜厚度。通过原子力显微镜(AFM)测量获得多层涂层的界面粗糙度,并在多层设计中模拟为均匀子层。最后,通过逆向工程AR涂层的光谱得到多层的厚度和折射率分布,并将其纳入AR涂层设计中。采用优化模型设计的193 nm AR涂层,经过理论与实验的光谱比较,取得了较好的符合性。此外,还获得了强曲率球面基底不同位置的折射率和厚度分布,通过同时优化球面基底不同位置的光谱,提高了沿径向的光谱均匀性。
2. 实验
本实验中的涂层使用了SYRUSpro-DUV涂层装置(莱宝光学,德国),该设备配备了行星旋转系统,且基板支架不倾斜。采用的基底为熔融石英片,表面粗糙度约为0.1 nm,厚度4 mm,直径25 mm。基底首先用混合乙醇和醚手工清洗,然后转移至真空室进行薄膜沉积。真空室通过干泵、冷冻泵和聚冷系统组合抽至基准压力2.0 × 10^-6 mbar。然后,用一组陶瓷加热器将基底加热至300 °C,并保持在该温度下2小时,之后用混合的氩气和氧气等离子体(100V)进行离子轰击清洗5分钟,最后进行薄膜沉积。LaF3和MgF2分别以0.6 nm/s和0.5 nm/s的沉积速率沉积到基底表面,沉积过程由石英晶体微天平进行监控。使用ML-6500分光光度计(Laser Zentrum Hannover,德国)在入射角10°下测量涂层样品的光学光谱。该分光光度计在真空条件下工作,真空压力为2.0 × 10^-6 mbar。使用氘灯(L7296,滨松光子,日本)作为光源,两个光电倍增管分别用于测量参考信号和实际信号的强度。反射光谱测量时,光束的大小大约为1 mm × 2 mm。通过调整样品的AOI(入射角)和信号探测器的位置来测量角分辨率反射率。光学吸收和散射损失通过193 nm激光热量计和193 nm集成散射测量仪(均由Laser Zentrum Hannover,德国开发)分别测量。表面粗糙度通过原子力显微镜(AFM,NaniteaAFM-110UM,瑞士)测量,AFM在常规大气环境下以敲击模式运行。扫描区域为2 μm × 2 μm。扫描线使用多项式函数进行拟合。对五个位置的测试样品进行测量,并通过对测量结果求均值得到均方根(rms)粗糙度。表面粗糙度、吸光度、散射损失和反射光谱在测试板的中心区域进行了测量。
本实验中制备并表征了三组样品。第一组为单层MgF2和LaF3薄膜,分别沉积在熔融石英基底和强曲率球面基底上。沉积的厚度范围为20 nm至35 nm(测试板上的沉积厚度),在球面基底上的沉积厚度为80 nm。单层薄膜的厚度和折射率通过逆向工程从其光学光谱中获得。第二组样品用于测定AR涂层的界面粗糙度,使用AFM分析每一界面的粗糙度。界面粗糙度通过多层结构的样品进行分析,结构为Sub/ L1/ L2/ .../ Li/ air,其中Sub表示熔融石英基底,Li表示AR涂层的第i子层的厚度。第三组样品为涂层/基底/涂层叠层结构(基底两面均为AR涂层)。通过逆向工程叠层的残余反射光谱获得子层的折射率。第二组和第三组样品均在测试板和球面基底上制备。对于测试板上的薄膜制备,熔融石英基底被放置在基底支架的中心位置,并且没有使用遮光掩膜。球面基底通过一个凸形夹具进行模拟,夹具的清晰孔径为220 mm,曲率半径为155 mm。夹具上有四个位置分别用于固定直径为25 mm的测试板,分别为P1、P2、P3和P4,位置距离夹具中心为45 mm、75 mm和105 mm。需要注意的是,测试板的涂层几何形状与球面基底的涂层几何形状在孔的中心位置相同。为提高球面基底上的薄膜厚度均匀性,遮光掩膜组被设置在基底下方大约10 mm的位置。通过遮光掩膜的校正,预计在模拟球面基底的凸形夹具中心区域,薄膜的厚度和折射率大致均匀。
3. 设计考虑
3.1 薄膜厚度的校准
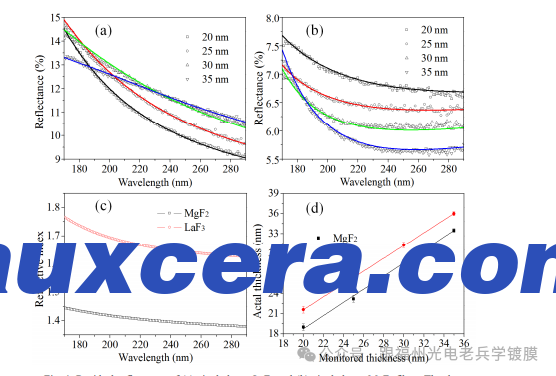
在我们的涂层装置中,石英晶体用于薄膜厚度监测的位置与行星旋转基底的位置不同。因此,监测到的薄膜厚度通常与基底上的实际薄膜厚度存在差异。通过实验,基底上的薄膜厚度是通过逆向工程计算涂层在测试板上的光学光谱获得的,测试板的位置与基底相同。图1(a)和图1(b)分别显示了沉积在熔融石英板一侧的单层LaF3和单层MgF2薄膜的反射光谱,监测的厚度范围为20 nm到35 nm。使用均匀单层模型,并根据Cauchy公式描述折射率的色散,逆向工程得到这些光谱[21]。图1(c)和图1(d)分别展示了测试板上薄膜的折射率和厚度。193 nm时,LaF3的折射率为1.718,MgF2的折射率为1.432,这与这些材料的体积折射率接近[21]。
沉积在测试板上的薄膜厚度(td)与监测的单层薄膜厚度(tm)呈线性关系,这一关系由以下公式描述:
td=I×tm+toolingt_d = I \times t_m + \text{tooling}td=I×tm+tooling
通过对实验数据进行线性拟合,得出MgF2和LaF3的I和tooling值分别为2.33和0.96,以及-0.8和0.98。非零的I值是由于在初始监测期内石英晶体的严重振荡造成的。类似的现象在先前通过石英晶体微天平监测氧化物涂层时也有报道[22]。根据公式(1),可以通过监测的厚度准确地确定实际的薄膜厚度。
图1. (a)单层LaF3和(b)单层MgF2薄膜的残余反射率。点表示实验测量数据,实线表示理论计算结果。红色、蓝色、黑色和绿色线条分别表示监测厚度为20 nm、25 nm、30 nm和35 nm的单层薄膜。(c)通过逆向工程实验反射光谱得到的LaF3(红色圆圈)和MgF2(黑色方块)的折射率色散。(d)测试板上沉积的单层LaF3(方块)和单层MgF2(圆圈)薄膜厚度与监测厚度的关系。线条为线性拟合结果。
3.2 界面粗糙度的影响
界面粗糙度是影响涂层光谱的一个重要因素,已知均介质理论能够很好地模拟界面粗糙度对单层金属氟化物薄膜(如MgF2 [23]、GdF3 [24]、LaF3 [25])以及多层涂层光谱的影响 [26]。在这里,我们将氟化物多层涂层中第i层和第(i+1)层之间形成的界面建模为一个均匀层,其厚度为
di=2σid_i = 2 \sigma_idi=2σi
折射率为
ni+1=ns,i+ns,i+12n_{i+1} = \frac{n_{s,i} + n_{s,i+1}}{2}ni+1=2ns,i+ns,i+1
其中,σi是第i层界面的粗糙度,ns,i 和 ns,i+1 分别表示倾向于第i界面的两种材料的折射率。由于人工界面亚层的存在,第i层和第(i+1)层的厚度必须分别减少σi,以保持总沉积量不变。需要注意的是,氟化物涂层的第i层贡献于第i层和第(i-1)层之间的两个界面。在考虑了界面σi和σ(i-1)之后,第i层的厚度(ti0)将从其沉积厚度(tdi)中调整为
ti0=tdi−σi−σi−1t_{i0} = t_{di} - \sigma_i - \sigma_{i-1}ti0=tdi−σi−σi−1
其中,σ0(即i=1时的σ(i-1))表示基底表面的粗糙度,用于计算第一个亚层的厚度。
3.3 薄膜孔隙率的影响
已知薄膜的孔隙率会影响193 nm AR涂层中亚层的折射率 [21]。在本研究中,孔隙率对薄膜折射率的影响可以通过以下公式描述:
ni2=nsi2(1−pi)+pi(ni2)n_i^2 = n_{si}^2 \left( 1 - p_i \right) + p_i \left( n_i^2 \right)ni2=nsi2(1−pi)+pi(ni2)
其中,ni和pi分别是第i层亚层的折射率和孔隙率,ns,i是相应的体材料的折射率。孔隙率还会影响亚层的厚度。对于体密度为ρ0的材料,薄膜的密度大约由(1 - pi)ρ0决定。由于厚度是通过沉积在石英晶体上的质量直接测量的,因此监测的厚度是体材料的厚度。当考虑到薄膜中的孔隙率时,实际的薄膜厚度(ti)应根据以下公式进行修正:
ti=tdi(1−pi)t_i = \frac{t_{di}}{(1 - p_i)}ti=(1−pi)tdi。
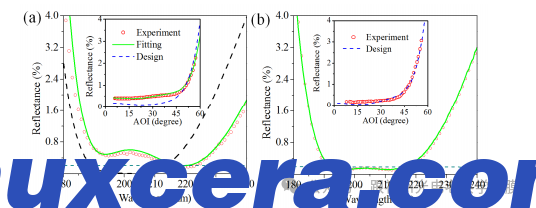
图2. 193 nm AR涂层在涂层/基底/涂层堆叠结构中的反射光谱和角度分辨反射率(插图)。图2(a)中的黑色(虚线)为使用Macleod软件进行的理论设计。红色点为测量得到的反射率,实线(绿色)表示考虑了界面粗糙度和亚层孔隙率变化后的反向工程光谱。图2(b)中的实线(绿色)和红色点分别为使用优化模型设计的堆叠结构的反射率和实验测量结果。
AR涂层的设计、制作和表征
在本研究中,通过氟化物多层膜实现了193 nm AR涂层,入射角范围为0°至60°,对于双面AR涂覆的熔融石英基板,残余反射率低于0.2%。我们首先使用商业软件(Macleod)设计AR涂层。设计中采用传统的多层模型,假设所有亚层为均匀的,界面为理想的。LaF3和MgF2亚层的折射率来自图1(c)。满足要求的典型涂层设计为:Sub/ 22.6 nm L/ 13.9 nm H/ 27.3 nm L/ 12.8 nm H/ 37.2 nm L/ 29.3 nm H/ 38.2 nm L/ air,其中H和L分别代表LaF3和MgF2亚层。图2(a)中的黑色虚线表示理论计算得到的涂层/基板/涂层堆叠的反射光谱。反射率在193 nm到215 nm之间低于0.2%。插图中的角度分辨反射率(蓝色虚线)表明,在AOI小于30°时,反射率低于0.2%。然而,在没有使用阴影掩膜进行厚度修正的测试板上准备的堆叠结构的测量残余反射率约为0.5%,范围为193 nm到208 nm,如图2(a)所示。相应地,图2(a)插图中显示的193 nm处的测量反射率(0.5%)在0°至30°的入射角范围内显著高于理论预测。实验与理论之间的显著差异表明,使用传统多层模型设计的193 nm AR涂层在实验中无法满足技术要求。此外,193 nm处的光学散射和吸收损失分别测得为0.04 ± 0.01%和0.71 ± 0.05%。
上述影响亚层折射率和厚度的三个因素必须在设计和制造具有低残余反射率(因此高透过率)的193 nm AR涂层时予以考虑。如表1所总结,实际沉积厚度(td)是通过公式(1)从监测厚度(tm)计算得出的。界面粗糙度(σ)通过AFM测量,其对多层结构的影响通过公式(2)-(4)进行描述。
表1. 193 nm AR涂层每个亚层的参数
准确确定亚层的折射率是分析AR涂层光谱的主要挑战。在本研究中,亚层的折射率和相应的薄膜孔隙率是通过反向工程多层光谱得到的。在反向工程过程中,由于193 nm AR涂层的亚层较薄,因此每个亚层内的折射率不均匀性可以忽略[21,27]。然而,由于折射率不均匀性,同一涂层材料制备的亚层的折射率是不同的。因此,在反向工程193 nm AR涂层的反射光谱时,将每个亚层的薄膜孔隙率作为拟合参数,使用公式(1)-(6)进行反向工程。采用模拟退火算法进行多参数优化。拟合后的光谱如图2(a)中的绿色实线所示。表1总结了通过反向工程结果得到的每个亚层在193 nm下的有效折射率和薄膜孔隙率。LaF3薄膜的孔隙率增长速度明显快于MgF2,这与LaF3单层膜比MgF2单层膜具有更高孔隙率的结果一致[21,28]。
AR涂层通过了解氟化物多层膜的折射率和厚度轮廓进行优化。涂层设计的性能通过优值函数(MF)进行评估。
优值函数(MF)计算公式为:
MF=w⋅T−∑Ai⋅num(7)MF = w \cdot T - \sum A_i \cdot \text{num} \quad (7)MF=w⋅T−∑Ai⋅num(7)
其中,num 为优化目标中的总点数,T_i 为目标值,A_i 为多层涂层的理论计算值,w_i 为第i个目标点的权重。
通过这种优化方法设计的典型涂层为:Sub/ 34.4 nm L/ 11.1 nm H/ 25.1 nm L/ 15.3 nm H/ 37.3 nm L/ 29.5 nm H/ 36.0 nm L/ air。此处厚度已经转换为监控厚度。图2(b)中的符号线和实线分别显示了涂层/基底/涂层堆叠的理论和实验残余反射光谱。与图2(a)中呈现的反射光谱相比,经过优化设计的涂层在193 nm至215 nm范围内表现出优异的AR性能。图2(b)插图中的角度分辨反射光谱与理论计算也高度一致。该双面AR涂层样品在193 nm时的散射损失和吸收损失分别为0.05 ± 0.01%和0.75 ± 0.05%,与传统设计样品的测量值略有不同,原因是膜厚(181.3 nm与188.7 nm)之间存在微小差异。
需要注意的是,如果亚层的厚度与初始设计偏差较大,接口粗糙度可能会与表1中给出的数值相差较大。此时,应重新测量接口粗糙度,以便进行理论反射光谱计算。该方法已被应用于其他涂层的设计和制造,所有这些涂层的实验光谱与理论计算结果都非常一致。
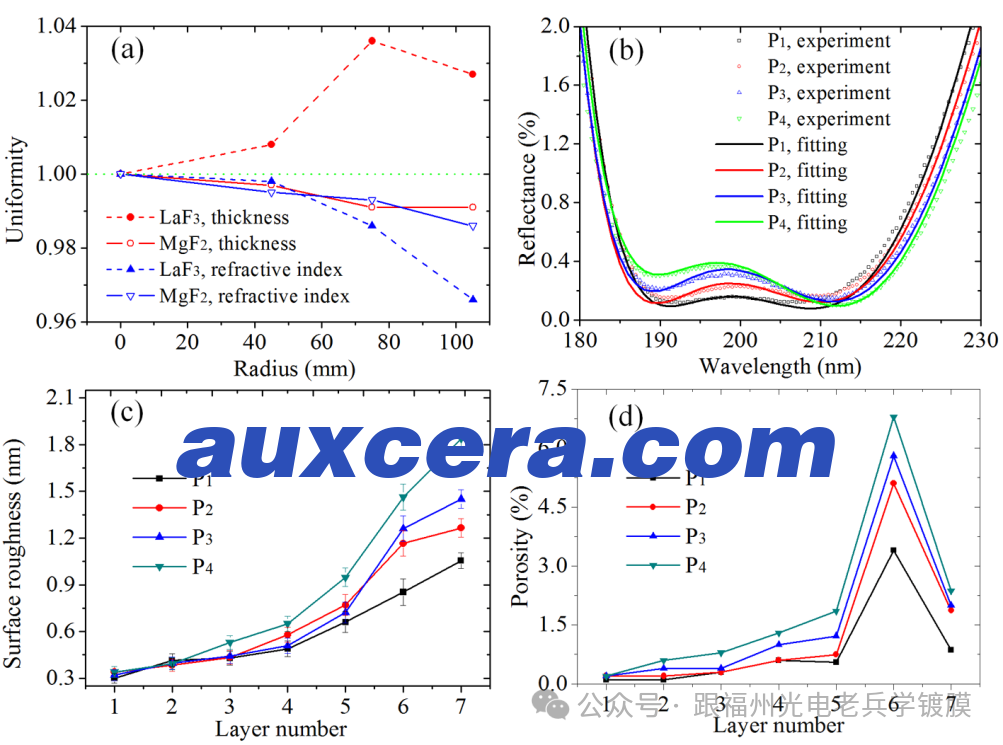
图3. (a) 单层LaF3和MgF2薄膜在球形基板上的厚度和折射率均匀性。
(b) 双面AR涂层样品在球形基板四个位置上的反射光谱,实验数据(符号)与反向工程数据(实线)。
(c) 和 (d) 分别展示了每个亚层的基于位置的接口粗糙度和孔隙率。
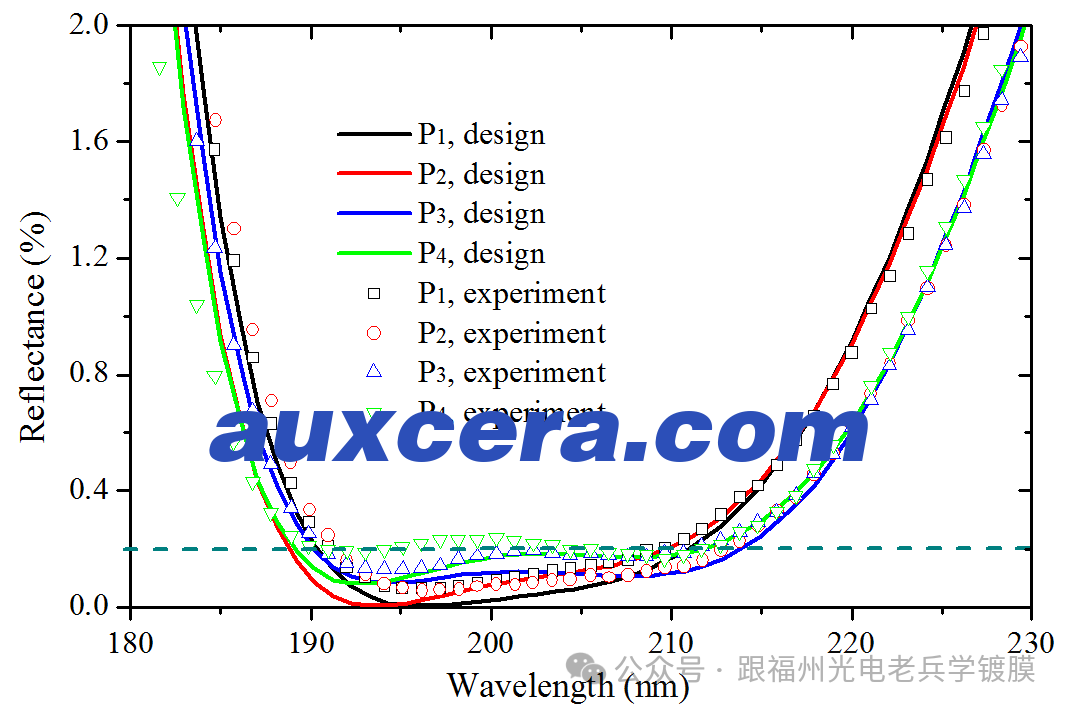
图4. 来自优化设计(实线)和实验(符号)在球形基板四个位置上的双面AR涂层熔融二氧化硅基板的反射光谱。虚线青色线表示0.2%的反射率。
结果与讨论
在我们的实验中,使用遮蔽掩模来修正强弯曲球形基板上的薄膜厚度不均匀性。通过遮蔽掩模,沉积在基板上的薄膜厚度与监测厚度之间的关系为:
tf=tm+I⋅toolingt_f = t_m + I \cdot \text{tooling}tf=tm+I⋅tooling
其中,因子fff 描述了遮蔽掩模的影响。为了确保tooling\text{tooling}tooling 和III 与公式(1)中的相同,在使用掩模之前,需要调整球形基板的高度,使其中心与测试板上的沉积高度相同。然后,因子fff 是通过单层薄膜在石英微天平上的监测厚度和使用遮蔽掩模后在球形基板中心的沉积厚度来确定的。
即使使用了遮蔽掩模进行薄膜厚度修正,单层LaF3和MgF2薄膜的特性仍然依赖于位置。图3(a)展示了在球形基板的P1-P4位置上,单层MgF2和LaF3薄膜厚度约为40nm时的折射率和厚度均匀性。这里的均匀性是通过与基板中心位置的厚度和折射率的对比来定义的。LaF3薄膜的厚度从中心逐渐增加,从1增加到约1.03,而MgF2薄膜的厚度从P1到P4逐渐减少,从1减小到0.99。在193nm处,折射率从基板的中心到边缘逐渐减小,尤其是单层LaF3薄膜。这与我们之前研究中厚单层薄膜的微观结构和光学特性一致[21]。
在使用遮蔽掩模进行厚度修正后,按照优化涂层设计制作的AR涂层堆叠被沉积在强弯曲的球形基板上。图3(b)展示了在球形基板的P1-P4位置上堆叠的反射光谱。结果表明,AR涂层的光谱性能强烈依赖于位置。差异在P4位置最为明显,此时残余反射率达到0.4%。图3(c)显示了相应位置上AR涂层的接口粗糙度。值得注意的是,基板边缘的接口粗糙度大于中心位置。例如,在P1和P4位置,S7的表面粗糙度分别为1.05 ± 0.05nm和1.84 ± 0.07nm。图3(d)展示了沿径向方向的亚层孔隙率。对于相同的亚层,薄膜的孔隙率也从基板的中心到边缘增加。从基板中心到边缘孔隙率的增加是由于柱状倾斜角度的增大,正如单一氟化物薄膜中所揭示的[21,29]。
通过同时优化不同位置的AR涂层性能,可以提高强弯曲基板上AR涂层的光谱均匀性。AR涂层在球形基板上的整体性能通过以下MF来评估:
MF′=1N∑j=1NMFjMF' = \frac{1}{N} \sum_{j=1}^{N} MF_jMF′=N1j=1∑NMFj
其中,N是球形基板上研究的位置数量。重要的是要限制每个亚层的厚度变化,以确保图3(c)中的接口粗糙度也能在优化设计中得到应用。得到的一个设计是Sub/33.2 nm L/11.5 nm H/26.0 nm L/17.6 nm H/39.2 nm L/31.5 nm H/36.4 nm L/air。图4中的实线和符号线分别表示在球形基板四个位置上AR涂层的理论和实验残余反射光谱。所有四个位置的反射率都低于或接近0.2%,远远优于图3(b)中呈现的结果,表明在设计具有宽AOI范围和强弯曲球形基板的AR涂层时,考虑厚度误差、接口粗糙度和薄膜孔隙率的重要性。
刘存定,孔名东,李彬成
光学与电子学研究所,中国科学院,成都 610209,中国
中国科学院大学,北京 100049,中国
电子科技大学,光电科学与工程学院,成都 610054,中国






留言咨询